Approaches to Calculating Number Needed to Treat (NNT) with Meta-Analysis
By Ken Koon Wong in statistics r R meta-analysis
October 28, 2023
Here, we have demonstrated three different methods for calculating NNT with meta-analysis data. I learned a lot from this experience, and I hope you find it enjoyable and informative as well. Thank you, @wwrighID, for initiating the discussion and providing a pivotal example by using the highest weight control event proportion to back-calculate ARR and, eventually, NNT. I also want to express my gratitude to @DrToddLee for contributing a brilliant method of pooling a single proportion from the control group for further estimation. Special thanks to @MatthewBJane, the meta-analysis maestro, for guiding me toward the correct equation to calculate event proportions, with weight estimated by the random effect model. 🙏

Image generated by DALL-E 3
Interesting Question
We all know how to calculate the Number Needed to Treat (NNT). It is calculated as one divided by the Absolute Risk Reduction (ARR), where ARR is the difference between the event proportions in the treatment and control groups. Meta-analysis is a powerful tool that aggregates the variability across multiple studies to provide a more precise estimate of the treatment effect and the event proportions in both the treatment and control groups. But the question remains: How do we calculate the NNT from the estimates obtained through meta-analysis?
Objectives:
- Prepare Data
- The Highest Weight Method
- Single Proportion Pooling Method Using Control Group Only
- Pooling From Full Meta-Analysis Method
- Comparison of All 3 Methods
- Exploring Other Meta-analysis Data & Compare The 3 Methods
- Acknowledgement
- Opportunities for improvement
- Lessons Learnt
Prepare Data
library(tidyverse)
library(meta)
library(kableExtra)
df1 <- tibble(study=c("bayliff 1999","pobble 2005","mavs 2006","dipom 2006","bbsa 2007","poise 2008"),event.c=c(0,5,21,2,0,215),n.c=c(50,48,250,459,109,4177))
df2 <- tibble(study=c("bayliff 1999","pobble 2005","mavs 2006","dipom 2006","bbsa 2007","poise 2008"),event.t=c(0,3,19,3,1,152),n.t=c(49,55,246,462,110,4174))
df <- df1 |>
full_join(df2, by = "study")
df |>
kable()
| study | event.c | n.c | event.t | n.t |
|---|---|---|---|---|
| bayliff 1999 | 0 | 50 | 0 | 49 |
| pobble 2005 | 5 | 48 | 3 | 55 |
| mavs 2006 | 21 | 250 | 19 | 246 |
| dipom 2006 | 2 | 459 | 3 | 462 |
| bbsa 2007 | 0 | 109 | 1 | 110 |
| poise 2008 | 215 | 4177 | 152 | 4174 |

The Highest Weight Method
One method is find the study with the most weight and narrow 95% confidence interval and use the event proportion of control groups and back-calculate NNT using pooled hazard ratio. This was shown by @wwrightID who
posted on an excellent review on how to do this.
For comparison, let’s only focus on the Secure trials
control <- 215/4177
hr <- 0.73
treatment <- hr * control
absolute_risk_reduction <- treatment - control
NNT <- 1/abs(absolute_risk_reduction) # turn negative number to positive
## NNT lower
hr_l <- 0.61
treatment_l <- hr_l * control
arr_l <- treatment_l - control
NNT_l <- ceiling(1/abs(arr_l))
## NNT upper
hr_u <- 0.88
treatment_u <- hr_u * control
arr_u <- treatment_u - control
NNT_u <- ceiling(1/abs(arr_u))
nnt_ci_1 <- paste0(round(NNT)," [95%CI ",NNT_l, "-",NNT_u,"]")
Our control event proportion is 0.0514723. Our calculated treatment event proportion is now 0.0375748. Our NNT with this method is 72 [95%CI 50-162]
Single Proportion Pooling Method Using Control Group Only
metap <- metaprop(event = event.c, n = n.c, data = df1, studlab = study, method.tau = "ML")
te_ran <- meta:::backtransf(metap$TE.common, sm = "PLOGIT")
treatment2 <- hr * te_ran
absolute_risk_reduction <- treatment2 - te_ran
NNT2 <- 1/abs(absolute_risk_reduction) # turn negative number to positive
## NNT lower
hr_l <- 0.61
treatment_l2 <- hr_l * te_ran
arr_l2 <- treatment_l2 - te_ran
NNT_l2 <- ceiling(1/abs(arr_l2))
## NNT upper
hr_u <- 0.88
treatment_u2 <- hr_u * te_ran
arr_u2 <- treatment_u2 - te_ran
NNT_u2 <- ceiling(1/abs(arr_u2))
nnt_ci_2 <- paste0(round(NNT2)," [95%CI ",NNT_l2, "-",NNT_u2,"]")
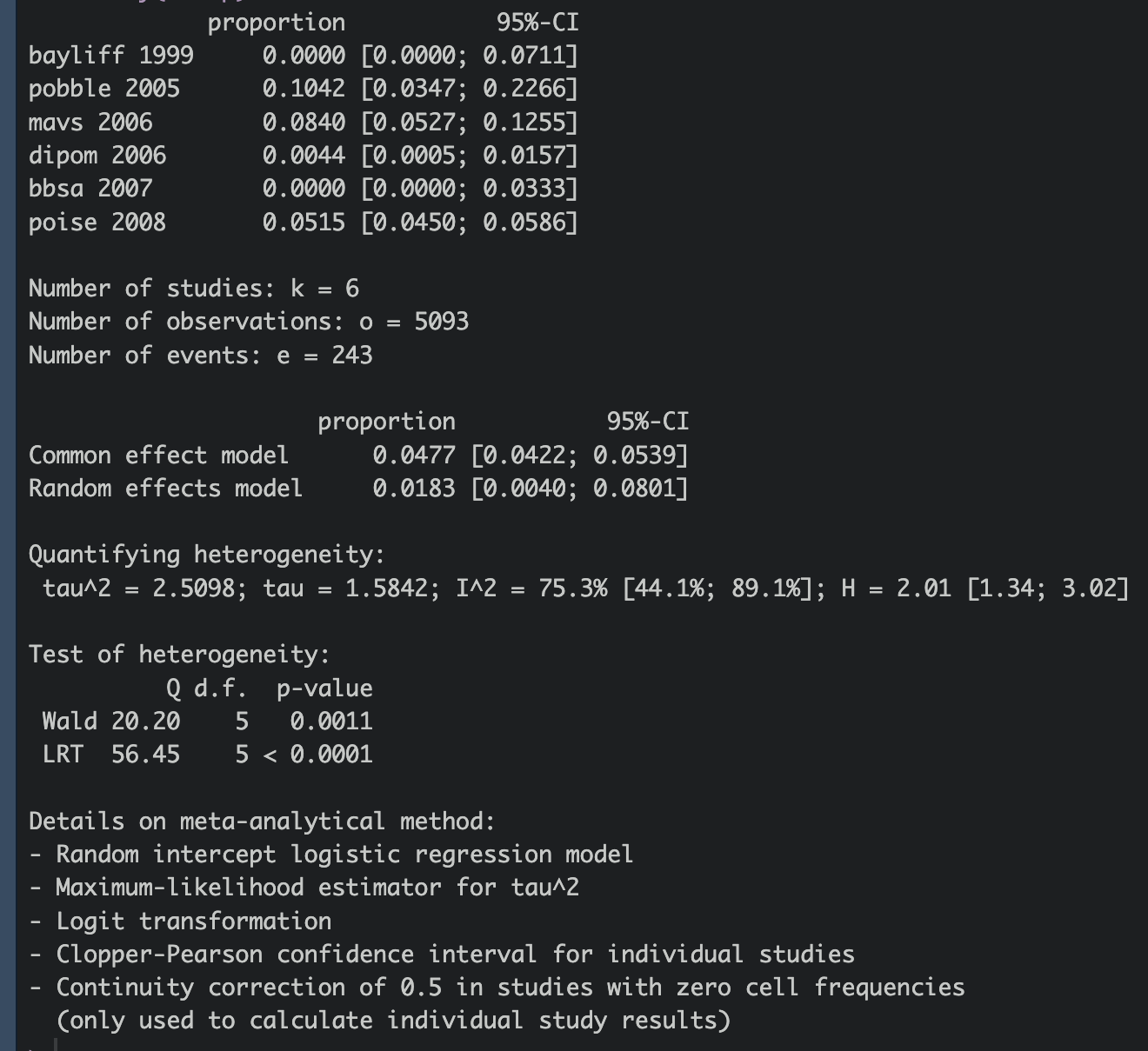 Our control event proportion is now 0.0477125. Our calculated treatment event proportion is now 0.0348302. Our NNT with single proportion pooling method is 78 [95%CI 54-175]. Take note that because Tau2 is very low, essentially means there is no heterogeneity between studies here, hence common model is used. If we had used random effect model here with tau2 of 0 and I2 of 0, our NNT became very large to 200+, give it a try!
Our control event proportion is now 0.0477125. Our calculated treatment event proportion is now 0.0348302. Our NNT with single proportion pooling method is 78 [95%CI 54-175]. Take note that because Tau2 is very low, essentially means there is no heterogeneity between studies here, hence common model is used. If we had used random effect model here with tau2 of 0 and I2 of 0, our NNT became very large to 200+, give it a try!
Too bad metaprop does not provide weights, see discussion
here.
But the alternative is
metap <- metaprop(event = event.c, n = n.c, data = df1, studlab = study, method = "Inverse", method.tau = "DL")
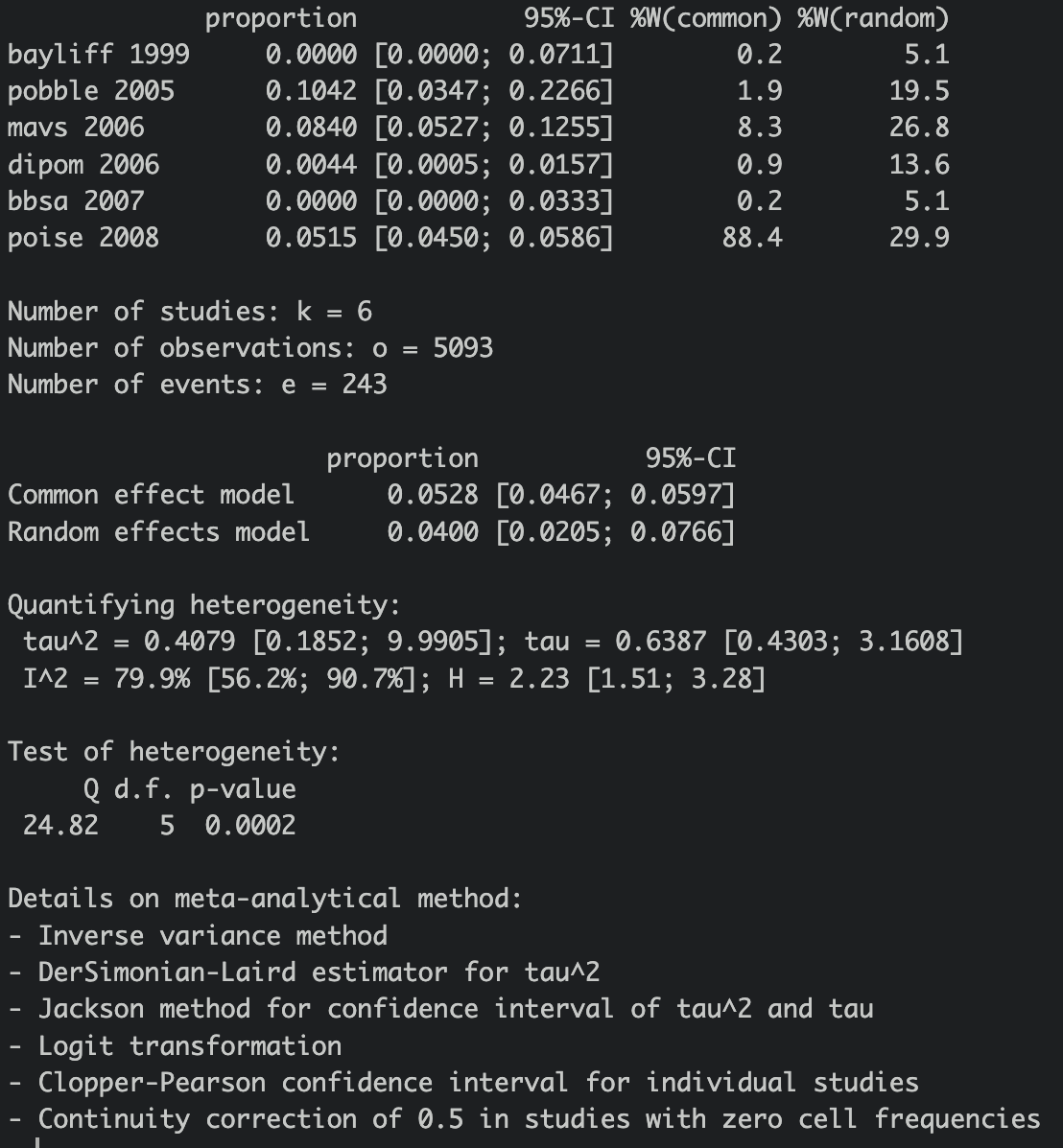
yes! We have weights. But wait, the proportion of event in control group in random effect model is not at all similar to the previous! I think mainly because of different method in calculating tau. Let’s stick with our previous
Pooling From Full Meta-Analysis Method
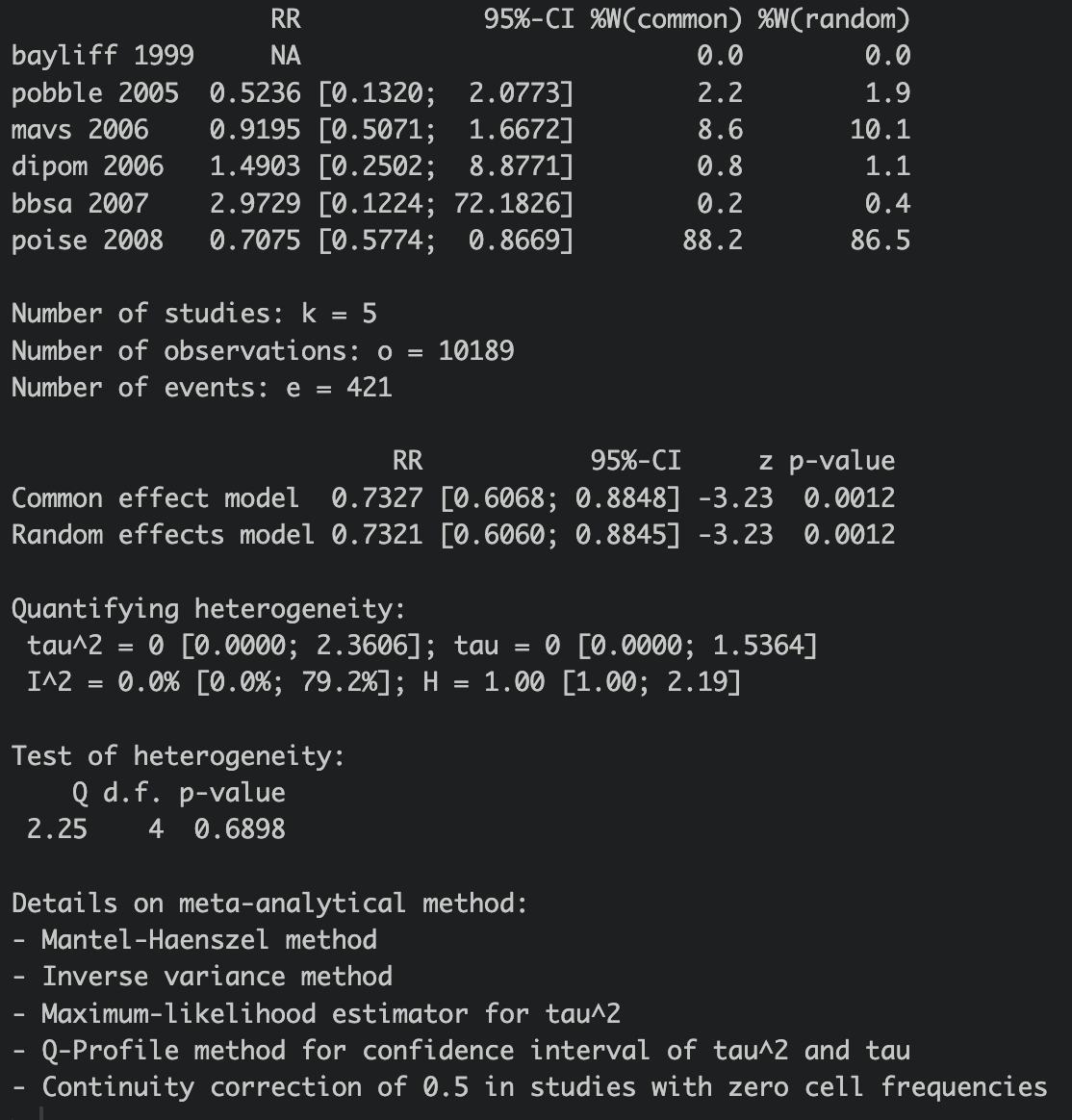
def <- metabin(event.c = event.c,n.c = n.c, event.e = event.t, n.e = n.t, studlab = study,data = df,sm="RR",level = 0.95,comb.fixed=T,comb.random=T,hakn = F)
summary(def)
Can We Reproduce Same Forest Plot?
forest(def)
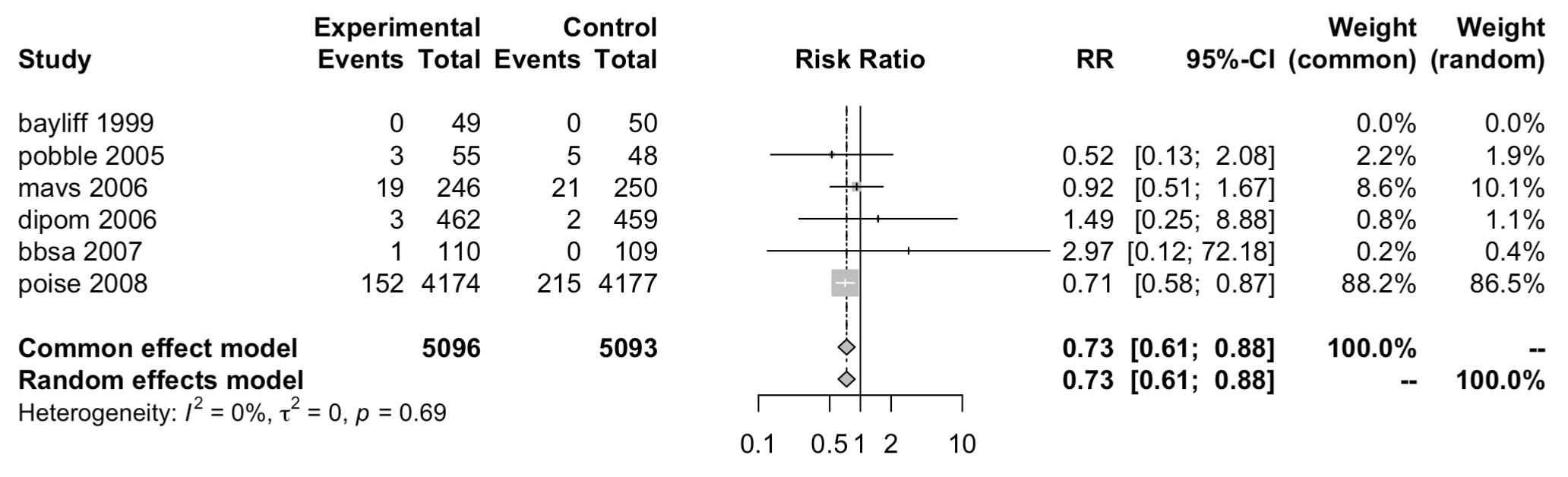 Not too shabby! Weights did not appear to be similar but the hazard ratio looks very similar, same with the 95% CI. Notice that there is lack of heterogeneity between studies, hence the fixed and random effect models are very similar.
Not too shabby! Weights did not appear to be similar but the hazard ratio looks very similar, same with the 95% CI. Notice that there is lack of heterogeneity between studies, hence the fixed and random effect models are very similar.
Let’s dive into calculating NNT with our last technique. But how?
# new dataframe with newly assigned weights
weights <- def$w.random / sum(def$w.random)
df_new <-
df |>
add_column(weights = weights) |>
mutate(total_weights = sum(weights),
log_t = log(event.t/n.t)*weights,
log_t = case_when(
is.infinite(log_t) ~ log(0.5/n.t)*weights, # Haldane-Anscombe correction
TRUE ~ log_t
)) |>
mutate(log_c = log(event.c/n.c)*weights,
log_c = case_when(
is.infinite(log_c) ~ log(0.5/n.c)*weights,
TRUE ~ log_c
)) |>
drop_na()
total_weights <- sum(df_new$weights)
# average event prop on treatment
prop_t <- exp(sum(df_new$log_t) / total_weights)
# average event prop control
prop_c <- exp(sum(df_new$log_c) / total_weights)
# RR random effect?
rr <- prop_t/prop_c
# arr
absolute_risk_reduction <- prop_t - prop_c
# NNT
NNT3 <- 1/abs(absolute_risk_reduction)
# NNT lower
var_arr <- prop_t * (1-prop_t) / sum(df_new$n.t) + prop_c * (1-prop_c) / sum(df_new$n.c)
nnt_l3 <- ceiling(1/abs(absolute_risk_reduction - 1.96*sqrt(var_arr)))
# NNT upper
nnt_u3 <- ceiling(1/abs(absolute_risk_reduction + 1.96*sqrt(var_arr)))
nnt_ci_3 <- paste0(ceiling(NNT3)," [95%CI ",nnt_l3, "-",nnt_u3,"]")
Our control event proportion is now 0.0528544. Our calculated treatment event proportion is now 0.0386394. Our NNT with single proportion pooling method is 71 [95%CI 45-165]. Very close to our first method! Mainly because the weights given on our random effect model highly favors poise 2018, it makes sense that our control event proportion should be quite similar to such!
The equation behind calculating the proportion for both treatment and control via its weight is:
$$\begin{gather} \ln(\text{prop}_t) = \sum \ln(\text{prop}_{it}) \cdot \text{weight}_{it} \\ \text{prop}_t = e^{\sum \ln(\text{prop}_{it}) \cdot \text{weight}_{it}} \end{gather}$$
\(prop_t\): overall proportion of treatment or control group.
\(prop_{it}\): proportion of ith study of treatment or control group (e.g,bbsa, poise).
\(weight_{it}\): random effect weights of ith study of treatment or control group.
This article is really helpful in calculating RR, OR, NNT lower and upper bounds.
How To Calculate NNT Lower and Upper Bound?
$$\begin{gather} \text{ARR} = \text{prop}_t - \text{prop}_c \\ var(\text{ARR}) = \frac{\text{prop}_t \cdot (1-\text{prop}_t)}{\text{n}_t} + \frac{\text{prop}_c \cdot (1-\text{prop}_c)}{\text{n}_c} \\ \text{ARR 95\% CI} = \text{ARR} \pm 1.96 \cdot \sqrt{\text{var}(\text{ARR})} \end{gather}$$
ARR: Absolute Risk Reduction.
\(var\): Variance.
\(prop_t\): Pooled Event Proportion in Treatment Group.
\(prop_c\): Pooled Event Proportion in Control Group.
CI: Confidence Interval, 95% preferred here, hence the z score of 1.96 used
Comparison of All 3 Methods
df_compare <- tibble(method=c("highest_weight","single_prop_pool","full"),prop_control=c(control,te_ran,prop_c),prop_treatment=c(treatment,treatment2,prop_t),nnt=c(nnt_ci_1,nnt_ci_2,nnt_ci_3),tau2=rep(def$tau2,3),I2=rep(def$I,3))
df_compare |>
kable()
| method | prop_control | prop_treatment | nnt | tau2 | I2 |
|---|---|---|---|---|---|
| highest_weight | 0.0514723 | 0.0375748 | 72 [95%CI 50-162] | 0 | 0 |
| single_prop_pool | 0.0477125 | 0.0348302 | 78 [95%CI 54-175] | 0 | 0 |
| full | 0.0528544 | 0.0386394 | 71 [95%CI 45-165] | 0 | 0 |
Exploring Other Meta-analysis Data & Compare The 3 Methods
Methenamine for Preventing UTI Without Renal Tract Abnormalities
Lee BS Cochrane Database Syst Rev 2012 Oct 17;10(10):CD003265

Using furness 1975 as our control given highest weight and narrow CI.
| method | prop_control | prop_treatment | nnt | tau2 | I2 |
|---|---|---|---|---|---|
| highest_weight | 0.2537313 | 0.0659701 | 5 [95%CI 5-21] | 0.8150958 | 0.6551118 |
| single_prop_pool | 0.2147027 | 0.0558227 | 6 [95%CI 6-25] | 0.8150958 | 0.6551118 |
| full | 0.2174201 | 0.0558707 | 7 [95%CI 5-10] | 0.8150958 | 0.6551118 |
Not too shabby! All 3 methods are quite similar in this heterogenous, low n studies. However, full method has a more narrow 95%CI of NNT. Interesting!
Multidisciplinary Teams for the Management of Infective Endocarditis: A Systematic Review and Meta-analysis
Roy AS Open Forum Infect Dis. 2023 Aug 21;10(9):ofad444. doi: 10.1093/ofid/ofad444..
Short-term mortality of patients with infective endocarditis
 Using Diab 2021 as our control given highest weight (10%) through random effect.
Using Diab 2021 as our control given highest weight (10%) through random effect.
| method | prop_control | prop_treatment | nnt | tau2 | I2 |
|---|---|---|---|---|---|
| highest_weight | 0.2567237 | 0.1540342 | 10 [95%CI 8-17] | 0.1465014 | 0.62777 |
| single_prop_pool | 0.2456502 | 0.1473901 | 10 [95%CI 8-18] | 0.1465014 | 0.62777 |
| full | 0.2428684 | 0.1448027 | 11 [95%CI 9-14] | 0.1465014 | 0.62777 |
All 3 methods appear to have very similar NNT, the only difference is 95% CI of NNT.
Effect of Corticosteroids on Mortality and Clinical Cure in Community-Acquired Pneumonia: A Systematic Review, Meta-analysis, and Meta-regression of Randomized Control Trials
Saleem N Chest. 2023 Mar;163(3):484-497. doi: 10.1016/j.chest.2022.08.2229..
The effect of adjuvant corticosteroid therapy on ICU admission
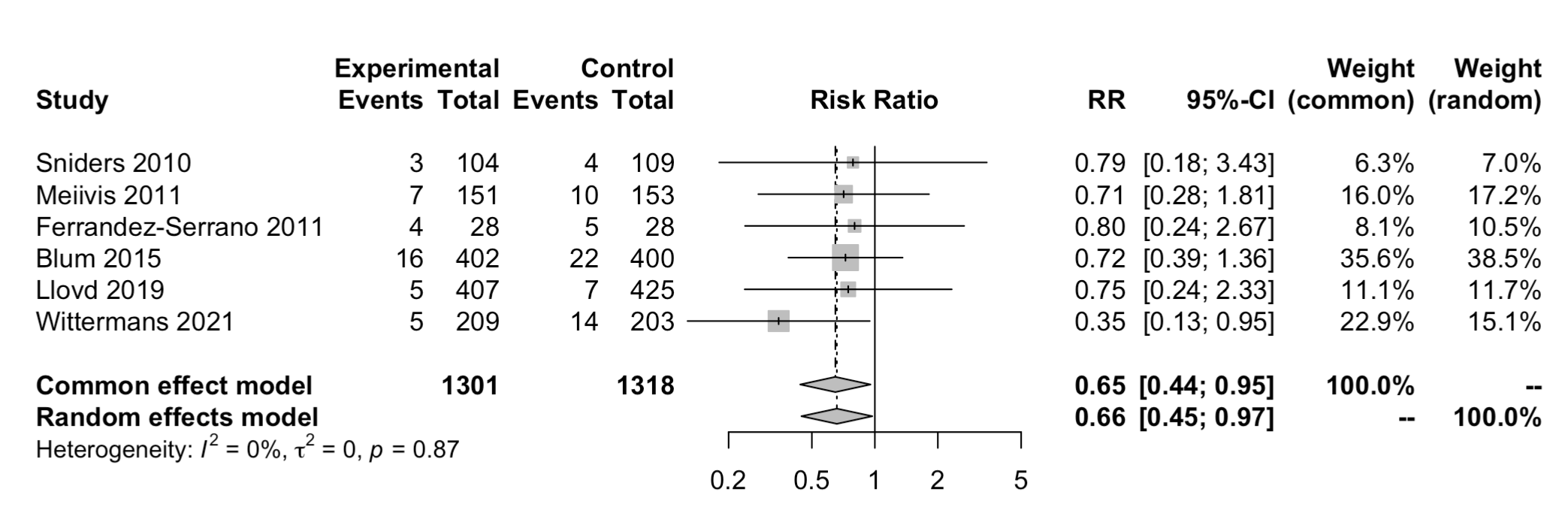
Using Blum 2015 with highest weight 38.5%.
| method | prop_control | prop_treatment | nnt | tau2 | I2 |
|---|---|---|---|---|---|
| highest_weight | 0.0550000 | 0.0363000 | 53 [95%CI 34-607] | 0 | 0 |
| single_prop_pool | 0.0515075 | 0.0339949 | 57 [95%CI 36-648] | 0 | 0 |
| full | 0.0559733 | 0.0368395 | 53 [95%CI 29-329] | 0 | 0 |
Both highest weight and full method have similar NNT. Slightly different for single proportion, but all quite similar for estimation. NNT lower and upper bound on this example has dramatic difference when full method is compared with highest weight and single proportion.
Acknowledgement
Thank you, @wwrighID, for initiating the discussion and providing a pivotal example by using the highest weight control event proportion to back-calculate ARR and, eventually, NNT. I also want to express my gratitude to @DrToddLee for contributing a brilliant method of pooling a single proportion from the control group for further estimation. Special thanks to @MatthewBJane, the meta-analysis maestro, for guiding us toward the correct equation to calculate event proportions, with weight estimated by the random effect model.
This discussion has been incredibly inspirational and educational! A heartfelt thank you to everyone involved for helping me answer a question that has intrigued me since 2021.
Opportunity for Improvement
- I am not certain if the 95%CI equation for both highest weight and single proportion is accurate. It made sense for the highest weight to use RR lower and upper bound and back calculate, but for the single proportion the
metapropactually provides a 95% interval for the proportion itself, should we than use these lower and upper bound and fix RR to back calculate treatment? 🤷♂️ If you do, please leave a comment below - Tackle odds ratio next. There are some great meta-analysis studies out there with OR as estimates. Shouldn’t be too hard, just need to be mindful about odds calculation and its more tedious conversion to proportion which eventually will need to calculate ARR and NNT.
- If you spot any mistakes, please feel free to send me a message, I’d love to learn from it!
Lessons learnt
- Learnt how to estimate NNT from all 3 methods (highest weight, single proportion pooling, full)
- I made an
Rscript of the function called
meta_compareusing all 3 methods if you’re interested
- I made an
Rscript of the function called
- Learnt how to calculate NNT lower and upper bound through variance of ARR
- Have to use
meta:::backtransfto convert random effect estimate - Learnt
\pmis\(\pm\)in latex, and add\in front of%in\text{} - Calculating pooled treatment and control group with its weight estimated by random effect model
- Finally, this answered my question I had since 2021, how to calculate NNT with meta-analysis!
If you like this article:
- please feel free to send me a comment or visit my other blogs
- please feel free to follow me on twitter, GitHub or Mastodon
- if you would like collaborate please feel free to contact me
- Posted on:
- October 28, 2023
- Length:
- 9 minute read, 1866 words
- Categories:
- statistics r R meta-analysis
- Tags:
- statistics r R meta-analysis