Front-door Adjustment
By Ken Koon Wong in causality r R front-door adjustment doCalculus
July 23, 2023
Front-door adjustment: a superhero method for handling unobserved confounding by using mediators (if present) to estimate causal effects accurately.

Let’s DAG an estimand!
library(dagitty)
dag <- dagitty('dag {
bb="0,0,1,1"
U [pos="0.402,0.320"]
X [exposure,pos="0.176,0.539"]
Y [outcome,pos="0.614,0.539"]
Z [pos="0.409,0.539"]
U -> X
U -> Y
X -> Z
Z -> Y
}
')
plot(dag)
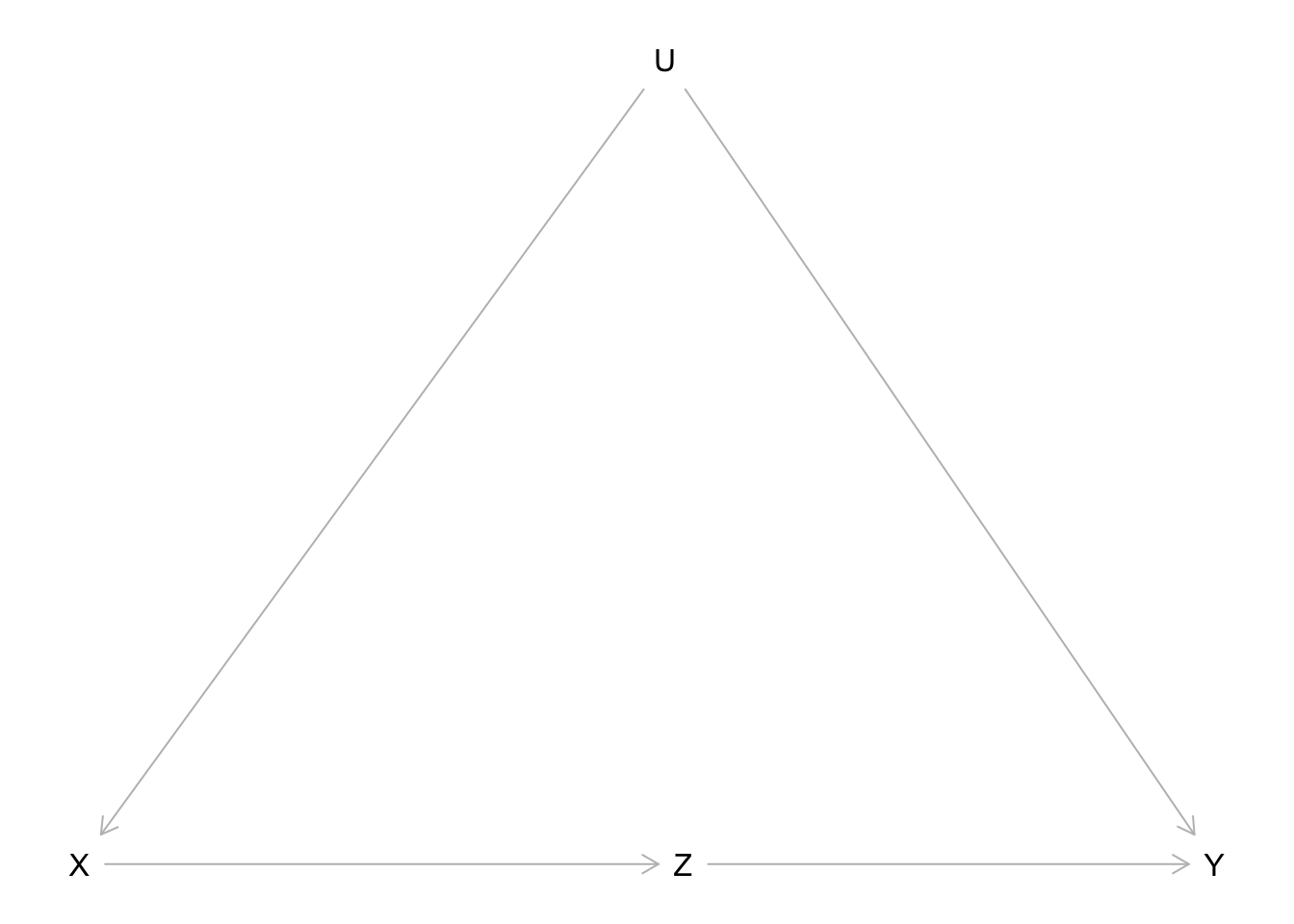
You can easily draw a DAG on
dagitty and then copy and paste the code and slot it in the dag { code } and voila!
X is our treatment variable.
Y is our outcome variable.
U is confounder that is not measured.
Z is our mediator.
Assume We Know The Truth
library(tidyverse)
library(DT)
# pseudorandomization
set.seed(1)
# Set sample
n <- 1000
# Set noise of each nodes
ux <- rnorm(n)
uy <- rnorm(n)
uz <- rnorm(n)
uu <- rnorm(n)
# Set each nodes' equation
u <- uu
x <- 0.4*u + ux
z <- 0.6*x + uz
y <- -0.5*z + uy + 0.6*u
# Create a table
df <- tibble(x=x,y=y,z=z,u=u)
# For easier viewing on blog
datatable(df)
The reason to assign uu, uy, uz, uu is basically to introduce some randomness to the equation. Then, the magic is when we write out the equations for u, x, z, y. This is what we meant by “knowing the truth”. We know exactly what coefficients for equations. For example, How much z would increase if there is an increase of 1 unit of x? The answer would be 0.6, as that is the coefficient we had set. We also know the exact u variable values are as well, but we’ll assume that we don’t and we’ll check if front-door adjustment can help us.
The Right Model ✅
In order for us to know what a wrong model is, we have to know what the right model is first. Since we know u, let’s model it and find the correct coefficient of x, holding u constant.
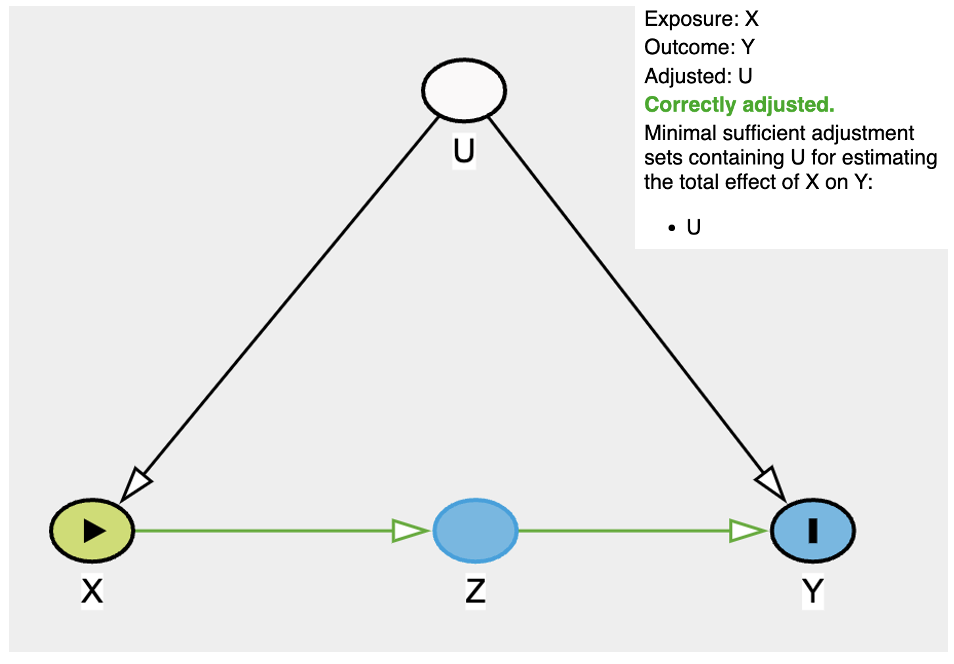
As you can see the screenshot above, if we have the luxury to adjust for u, then we have essentially d-seperated x and y and we can estimate their coefficient. Let’s put in into linear regression model.
correct_model <- lm(y~x+u,df)
summary(correct_model)
##
## Call:
## lm(formula = y ~ x + u, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4698 -0.7571 -0.0529 0.7869 3.8100
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.02431 0.03641 -0.668 0.505
## x -0.31841 0.03520 -9.045 <2e-16 ***
## u 0.61805 0.03810 16.220 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.151 on 997 degrees of freedom
## Multiple R-squared: 0.2142, Adjusted R-squared: 0.2126
## F-statistic: 135.8 on 2 and 997 DF, p-value: < 2.2e-16
Looking at the coefficient for x, the correct estimate is -0.3184144
The Wrong Model ❌
Now, let’s look at the wrong model. Let’s say naively, we want to fit just y ~ x. What would happen?
model_no_front <- lm(y~x,df)
summary(model_no_front)
##
## Call:
## lm(formula = y ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1379 -0.8724 -0.0593 0.9068 4.0849
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.01287 0.04091 -0.315 0.75319
## x -0.09505 0.03641 -2.611 0.00917 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.294 on 998 degrees of freedom
## Multiple R-squared: 0.006784, Adjusted R-squared: 0.005789
## F-statistic: 6.817 on 1 and 998 DF, p-value: 0.009167
Did you notice that the x coefficient is -0.0950511 ?
Let’s look at another wrong model, let’s control for Z and see what that shows?
model <- lm(y~z+x,df)
summary(model)
##
## Call:
## lm(formula = y ~ z + x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0450 -0.8006 0.0104 0.8316 3.9043
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.005363 0.037782 -0.142 0.887
## z -0.483048 0.036701 -13.162 < 2e-16 ***
## x 0.216663 0.041125 5.268 1.69e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.195 on 997 degrees of freedom
## Multiple R-squared: 0.1538, Adjusted R-squared: 0.1521
## F-statistic: 90.61 on 2 and 997 DF, p-value: < 2.2e-16
Wait, what? Now x is 0.2166626 ??? The correct coefficient is -0.3184144 as we previously had calculated. What is going on here? 🤪
Here is a screenshot of wrongly adjusting for z
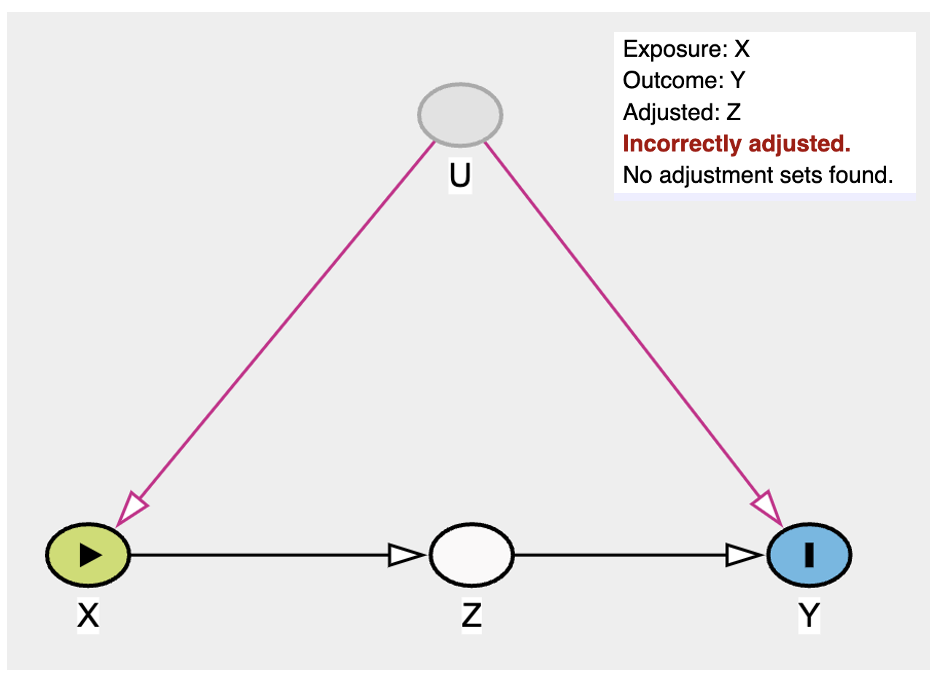
What do we do? 🤷♂️
In Comes The Front-door Adjustment! If we’re lucky… 🍀
Let’s look at the equation to calculate for front-door adjustment. It is divided into 2 steps
1. Estimate Z and do(X)
The game of doCalculus is to how to get rid of the
do
\(p(Z|do(X)) = \sum p(Z|X)\).
Why is the above estimate true? Let’s go back to the DAG and change outcome to z
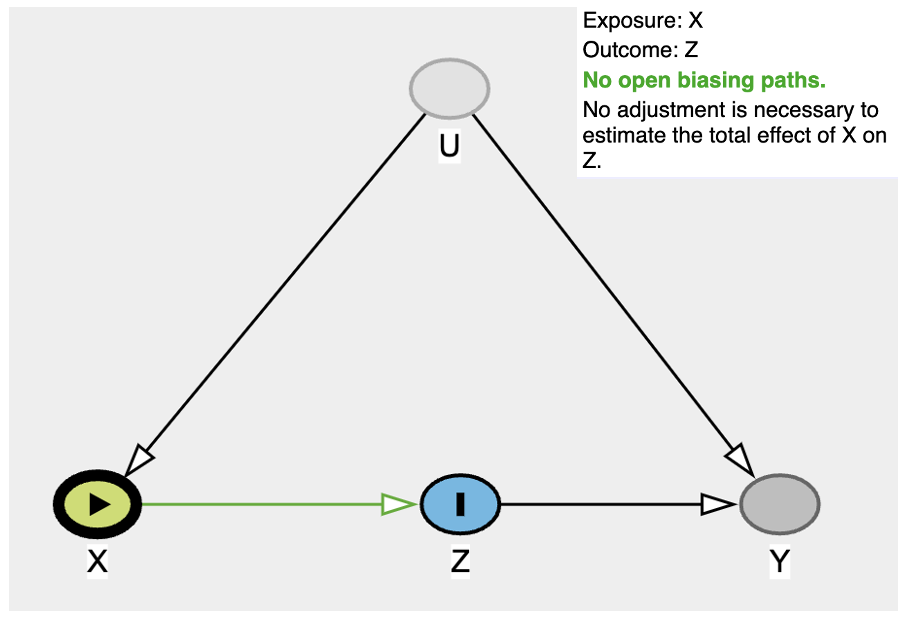 Did you notice that there is no need to adjust anything at all because there is a collider on
Did you notice that there is no need to adjust anything at all because there is a collider on y ? Can’t see it? Here you go: z -> y <- u -> x. Sometimes writing the equation out really helps.
# 1. Estimate Z and do(X)
model2 <- lm(z~x,df)
summary(model2)
##
## Call:
## lm(formula = z ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5756 -0.6448 -0.0196 0.7013 2.7987
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.01553 0.03258 0.477 0.634
## x 0.64531 0.02900 22.254 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.03 on 998 degrees of freedom
## Multiple R-squared: 0.3317, Adjusted R-squared: 0.331
## F-statistic: 495.2 on 1 and 998 DF, p-value: < 2.2e-16
x coefficient is 0.6453056.
2. Estimate Y and do(Z)
\(p(Y|do(Z)) = \sum p(Y|Z,X).p(X)\).
Why is the above estimate true? Let’s go back to the DAG and change outcome to y and exposure to z
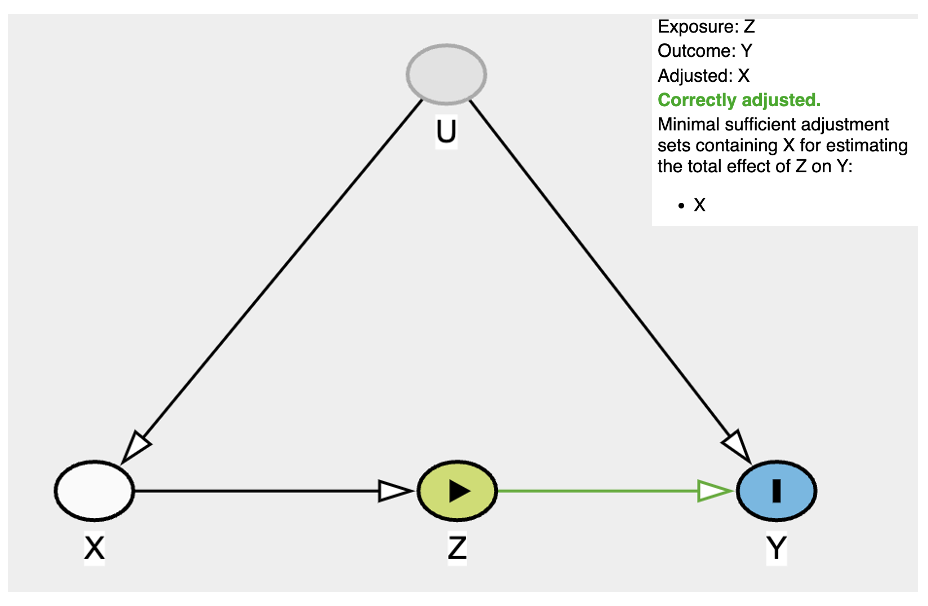 Did you notice that we need to adjust for one node that we actually have data on to achieve d-separation? Can’t see it? Here you go:
Did you notice that we need to adjust for one node that we actually have data on to achieve d-separation? Can’t see it? Here you go: y <- u -> x -> z. What is it? x !!! The treatment itself, how uncanny !!!
Let’s check out this model
model <- lm(y~z+x,df)
summary(model)
##
## Call:
## lm(formula = y ~ z + x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0450 -0.8006 0.0104 0.8316 3.9043
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.005363 0.037782 -0.142 0.887
## z -0.483048 0.036701 -13.162 < 2e-16 ***
## x 0.216663 0.041125 5.268 1.69e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.195 on 997 degrees of freedom
## Multiple R-squared: 0.1538, Adjusted R-squared: 0.1521
## F-statistic: 90.61 on 2 and 997 DF, p-value: < 2.2e-16
z coefficient is -0.4830482.
3. Put it together - x coefficient * z coefficient
The true x coefficient in relation to y is essentially the multiplication of the above estimates!
\(p(Y|do(X)) = p(Y|do(Z)).p(Z|do(X)) = \sum p(Y|Z,X').p(X').\sum p(Z|X)\)
Let’s see if this is true with our codes and data
#correct estimated coefficient
model$coefficients[["z"]]*model2$coefficients[["x"]]
## [1] -0.3117137
Our estimate x coefficient is -0.3117137. Whereas our true x coefficient is -0.3184144. About 0.0067008 difference. Not too shabby at all !!! Notice that we did not need u data at all to estimate this. Awesomeness!!!

Yes, it’s not going to be exactly what the true estimate is but it’s close enough! You can mess around the n by increasing it and you will then get closer to the true estimate. Also depends on your set.seed, the true coefficient will be different too, give seed 123 a try.
Why Coef Z * Coef X??? Addendum 2-23-24
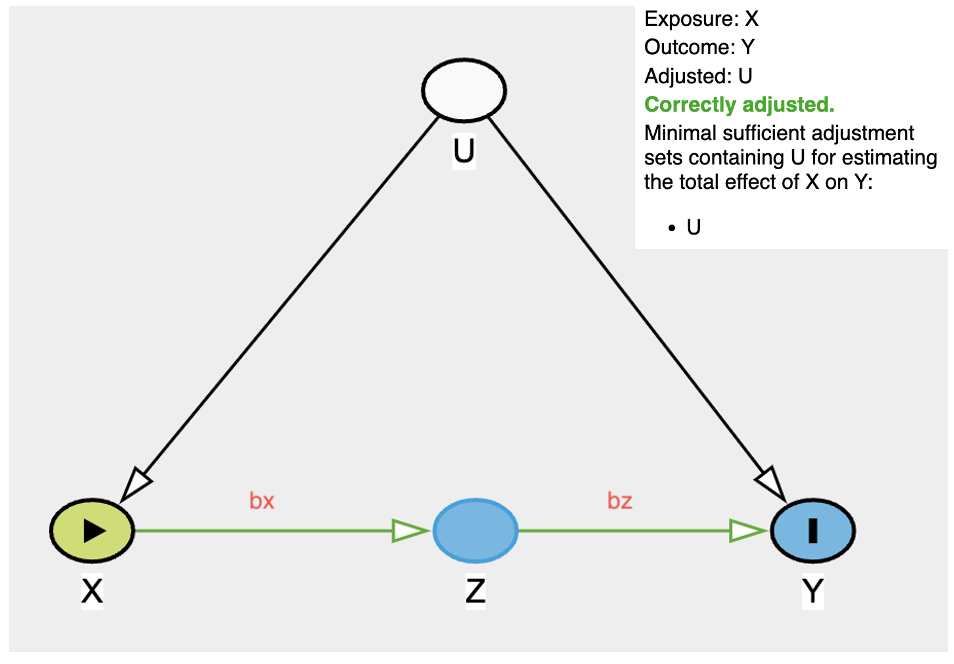 Looking at the DAG above, we want to estimate the effect of X to Y. The simple equation of X -> Z and Z -> Y would be below. The question is, why are we multiplying
Looking at the DAG above, we want to estimate the effect of X to Y. The simple equation of X -> Z and Z -> Y would be below. The question is, why are we multiplying bx and bz as shown in the above front door method? Take a look at the equations below.
\begin{gather} \text{Z} = \text{bx}\cdot\text{X} \\ \text{Y} = \text{bz}\cdot\text{Z} \\ Y = bz \cdot (bx \cdot X) \\ Y = bz \cdot bx \cdot X \end{gather}
Hence, to find the effect of X to Y, is basically derivative of Y with respect to X, which is bx (x coefficient in model2, the 1st front door method step) multiplies by bz (coefficient z in model, the 2nd front door method step).
Lessons learnt
- Front-door analysis is another great tool when unobserved confounder is a problem
- Learnt how to estimate front-door formula from scratch is very helpful in understanding how the whole thing works
- To estimate whether a method is beneficial we can simulate equations and data and test the theory
- there are other packages such as doWhy which will calculate all these for you without a hassle in deriving your own formula
If you like this article:
- please feel free to send me a comment or visit my other blogs
- please feel free to follow me on twitter, GitHub or Mastodon
- if you would like collaborate please feel free to contact me
- Posted on:
- July 23, 2023
- Length:
- 8 minute read, 1560 words
- Categories:
- causality r R front-door adjustment doCalculus