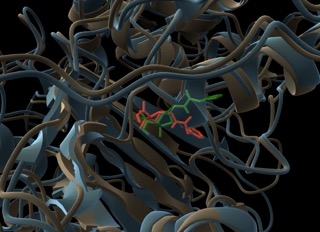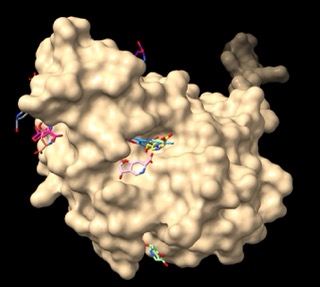
Assessing TEM, CTX-M, and KPC-2 With Molecular Docking and Molecular Dynamic Simulation
🧬 Testing beta-lactamase resistance with AlphaFold + DiffDock + GROMACS! Watch clavulanic acid bind TEM-5, CTX-M-15, KPC-2, and get rejected by TEM-30. Simulation confirms biology! 🔬💊