The 100 Prisoners Problem

Brief Introduction:

The 100 prisoners problem is a probability theory and combinatorics problem. In this challenge, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive.

Rules:

• We have 100 prisoners labeled: 1, 2 … 100 on their clothes
• we have a room filled with 100 boxes labeled 1, 2, … 100 on the outside of the boxes
• inside each box, there is a number from 1, 2 … 100
• only 1 prisoner may enter the room each time
• Each prisoner may open only up to 50 attempts/boxes and cannot communicate with other prisoners
• if the prisoner found his/her/their number, he/she/they will exit the room and no be able to talk to other prisoners. Same thing if he/she/they cannot find their number
• All prisoners MUST find their number in order to win the game

Question:

What is the best strategy to maximize probability of winning the game?

Answer:

Suprisingly… with Loop strategy… 30.68528% !!! click on the image to link to awesome Veritasium video

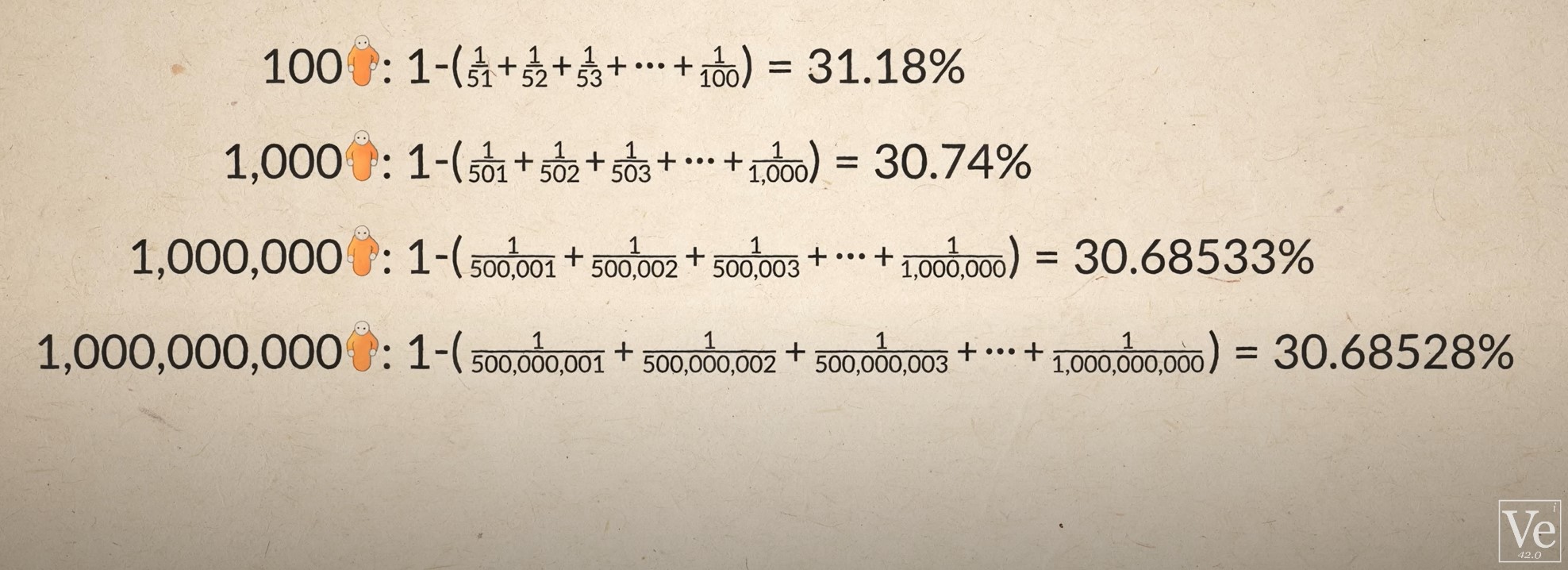
Let’s try to simulate this

1. Set up an empty dataframe

library(tidyverse)

total_n <- 1000
df <- tibble(trial=as.numeric(),prob=as.numeric())

• load tidyverse
• set total_n of trial to run
• create an empty dataframe called df that gives us:
  • column 1 trial as the number of trial
  • column 2 prob as the probability of success

2. Set up for loop of trials

for (i in c(1:total_n)) {

true <- 0 # count how prisoner got right per trial  
n <- 1000
count <- 0 # count how many winning trials (meaning if all 100 prisoners got the number right)

for (i in c(1:n)) {

ranbox <- sample(1:100,100,replace=F) 
# randomly assign 1 through 100 (this would be the boxes in the room)


for (i in c(1:100)) {     
    j <- 1  # this is label for jth attempt
    i <- i # this is label for prisoner number  

  while (TRUE) {
    if (j==1) {   
      go <- ranbox[i]
      base <- go
      j <- j + 1
      # See comment 2.41
      
    }
    if (j>50) { 
      
      true <- 0 
      break
      # see comment 2.42
      
      }
    if (j>1) {
      go <-ranbox[go]
      j <- j + 1
      # see comment 2.43
      
      
    }
    if (go==i) {
      true <- true + 1

      break
      # see comment 2.44
    }
    if (base==go) { 

      break
      # see comment 2.45
    }
    if (true==100) { 
      count <- count + 1
      true <- 0
      # see comment 2.46
      }
  
    
  }
}
} 
# probability of ith trial per experiment
prob <- count / n 

# add the trial and result of probability to the empty dataframe
df <- df %>%
  add_row(tibble(trial=i,prob=prob))

}

# save the dataframe since it took so long to run, uncomment the code below
# save(df, file = "df_prisoner_prob.Rda")

Wow, there is so much to unpack here. Let’s break it down

• There are 4 loops in here:
  • 2.1 For loop of trials 1 … total_n which is 1000
    • 2.2 For loop of trials of 1 … n which is 1000 as well
      • 2.3 For loop of 1 … 100 prisoner entering the room (labelled as i)
        • 2.4. Conditional while loops (each attempt is labelled as j):
          • 2.41 if j is 1 (which is first attempt of prisoner ith), pick from ranbox and assign it to go and set base as go as well
          • 2.42 if j > 50 (meaning at the 50th attempt of opening the box by prisoner ith), then set true as 0 (meaning this prisoner did not get the number)
          • 2.43 this code runs when j is 2 or more (which is 2nd or more attempt of prionser ith) by going to box with number go and assign the new number go. Meaning, if the first box is number 20, the prisoner will go to box 20 which is index 20 of ranbox which contains a different number and assign go with that new number to go next
          • 2.44 if the ith prisoner’s first box is the same number then increase true by 1 point
          • 2.45 if base == go then break. Meaning like what the theory suggests, if jth attempt goes back to the number from the first box then stop, considering that the prisoner did not get it right
          • 2.46 if all prisoner got them right, then increase count by 1 and reset true to zero

If still unclear, look through the video for the strategy, then re-read or even better run the code to get an understanding !

Essentially, the code above will take some time about to run, you should then save it for your reference

3. Let’s take a look at the df dataframe

load(file = "df_prisoner_prob.Rda")

# calculating median and 95% Confidence interval
med <- paste0("median:", 
              df$prob %>% median(), 
              " [95%CI ", 
              df$prob %>% quantile(0.025),
              "-",
              df$prob %>% quantile(0.0975),"]")

# plotting it
df %>%
  ggplot(aes(x=prob)) +
  geom_histogram(alpha = 0.5) +
  theme_bw() +
  ggtitle(paste0("Histogram of probability of winning the prisoner game (trial of ",total_n,")")) +
  annotate(
    "text", label = med,
    x = 0.3, y = 5, size = 5, colour = "black"
  )

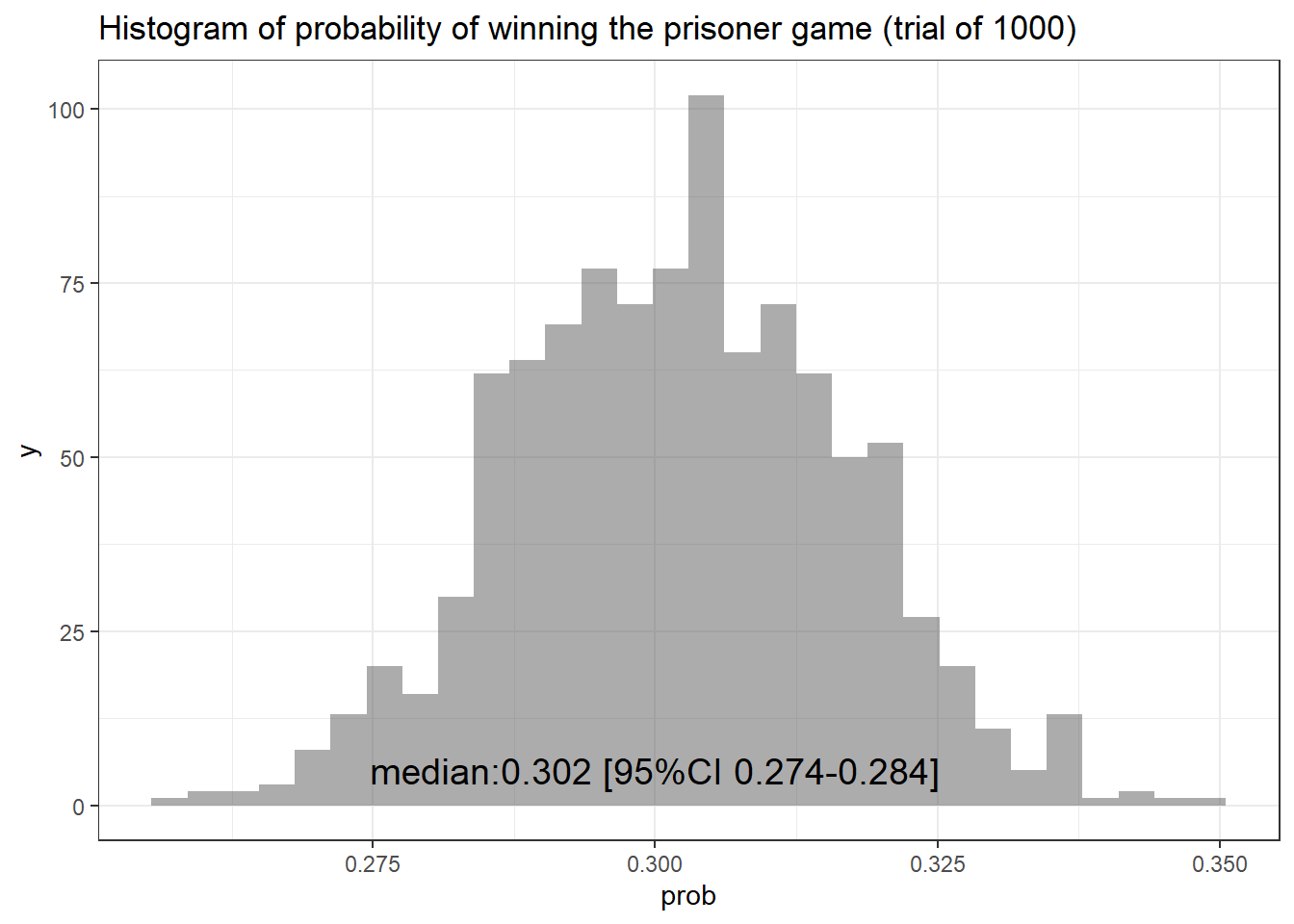
Pretty cool, eh!

Conclusion/Lessons learnt:

If you can’t formulate, simulate! :D Thanks to my brother, Ken S’ng Wong for introducing me to Veritasium video of this topic. Interesting problem to simulate. I’m sure there is a simpler code to simulate it, but I have to make it complicated. lol